6. Kesten Processes and Firm Dynamics#

GPU

This lecture was built using a machine with JAX installed and access to a GPU.

To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.

To run this lecture on your own machine, you need to install Google JAX.

In addition to JAX and Anaconda, this lecture will need the following libraries:

!pip install quantecon

6.1. Overview#

This lecture describes Kesten processes, which are an important class of stochastic processes, and an application of firm dynamics.

The lecture draws on an earlier QuantEcon lecture, which uses Numba to accelerate the computations.

In that earlier lecture you can find a more detailed discussion of the concepts involved.

This lecture focuses on implementing the same computations in JAX.

Let’s start with some imports:

import matplotlib.pyplot as plt
import quantecon as qe
import jax
import jax.numpy as jnp
from jax import random
from jax import lax
from quantecon import tic, toc
from typing import NamedTuple
from functools import partial

Let’s check the GPU we are running

!nvidia-smi

Mon Nov 17 03:41:42 2025       
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 575.51.03              Driver Version: 575.51.03      CUDA Version: 12.9     |
|-----------------------------------------+------------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id          Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |           Memory-Usage | GPU-Util  Compute M. |
|                                         |                        |               MIG M. |
|=========================================+========================+======================|
|   0  Tesla T4                       Off |   00000000:00:1E.0 Off |                    0 |
| N/A   31C    P8             13W /   70W |       0MiB /  15360MiB |      0%      Default |
|                                         |                        |                  N/A |
+-----------------------------------------+------------------------+----------------------+
                                                                                         
+-----------------------------------------------------------------------------------------+
| Processes:                                                                              |
|  GPU   GI   CI              PID   Type   Process name                        GPU Memory |
|        ID   ID                                                               Usage      |
|=========================================================================================|
|  No running processes found                                                             |
+-----------------------------------------------------------------------------------------+

6.2. Kesten processes#

A Kesten process is a stochastic process of the form

(6.1)#

X_{t + 1} = a_{t + 1} X_{t} + η_{t + 1}

where ${a_{t}}_{t \geq 1}$ and ${η_{t}}_{t \geq 1}$ are IID sequences.

We are interested in the dynamics of ${X_{t}}_{t \geq 0}$ when $X_{0}$ is given.

We will focus on the nonnegative scalar case, where $X_{t}$ takes values in $R_{+}$ .

In particular, we will assume that

the initial condition $X_{0}$ is nonnegative,
${a_{t}}_{t \geq 1}$ is a nonnegative IID stochastic process and
${η_{t}}_{t \geq 1}$ is another nonnegative IID stochastic process, independent of the first.

6.2.1. Application: firm dynamics#

In this section we apply Kesten process theory to the study of firm dynamics.

6.2.1.1. Gibrat’s law#

It was postulated many years ago by Robert Gibrat that firm size evolves according to a simple rule whereby size next period is proportional to current size.

This is now known as Gibrat’s law of proportional growth.

We can express this idea by stating that a suitably defined measure $s_{t}$ of firm size obeys

(6.2)#

\frac{s_{t + 1}}{s_{t}} = a_{t + 1}

for some positive IID sequence ${a_{t}}$ .

Subsequent empirical research has shown that this specification is not accurate, particularly for small firms.

However, we can get close to the data by modifying (6.2) to

(6.3)#

s_{t + 1} = a_{t + 1} s_{t} + b_{t + 1}

where ${a_{t}}$ and ${b_{t}}$ are both IID and independent of each other.

We now study the implications of this specification.

6.2.1.2. Heavy tails#

If the conditions of the Kesten–Goldie Theorem are satisfied, then (6.3) implies that the firm size distribution will have Pareto tails.

This matches empirical findings across many data sets.

But there is another unrealistic aspect of the firm dynamics specified in (6.3) that we need to address: it ignores entry and exit.

In any given period and in any given market, we observe significant numbers of firms entering and exiting the market.

In this setting, firm dynamics can be expressed as

(6.4)#

s_{t + 1} = e_{t + 1} 1 {s_{t} < \bar{s}} + (a_{t + 1} s_{t} + b_{t + 1}) 1 {s_{t} \geq \bar{s}}

The motivation behind and interpretation of (6.4) can be found in our earlier Kesten process lecture.

What can we say about dynamics?

Although (6.4) is not a Kesten process, it does update in the same way as a Kesten process when $s_{t}$ is large.

So perhaps its stationary distribution still has Pareto tails?

We can investigate this question via simulation and rank-size plots.

The approach will be to

generate $M$ draws of $s_{T}$ when $M$ and $T$ are large and
plot the largest 1,000 of the resulting draws in a rank-size plot.

(The distribution of $s_{T}$ will be close to the stationary distribution when $T$ is large.)

In the simulation, we assume that each of $a_{t}, b_{t}$ and $e_{t}$ is lognormal.

Here’s a class to store parameters:

class Firm(NamedTuple):
    μ_a:   float = -0.5
    σ_a:   float = 0.1
    μ_b:   float = 0.0
    σ_b:   float = 0.5
    μ_e:   float = 0.0
    σ_e:   float = 0.5
    s_bar: float = 1.0

Here’s code to update a cross-section of firms according to the dynamics in (6.4).

@jax.jit
def update_cross_section(s, a, b, e, firm):
    μ_a, σ_a, μ_b, σ_b, μ_e, σ_e, s_bar = firm
    s = jnp.where(s < s_bar, e, a * s + b)
    return s

Now we write a for loop that repeatedly calls this function, to push a cross-section of firms forward in time.

For sufficiently large T, the cross-section it returns (the cross-section at time T) corresponds to firm size distribution in (approximate) equilibrium.

def generate_cross_section(
        firm, M=500_000, T=500, s_init=1.0, seed=123
    ):

    μ_a, σ_a, μ_b, σ_b, μ_e, σ_e, s_bar = firm
    key = random.PRNGKey(seed)

    # Initialize the cross-section to a common value
    s = jnp.full((M, ), s_init)

    # Perform updates on s for time t
    for t in range(T):
        key, *subkeys = random.split(key, 4)
        a = μ_a + σ_a * random.normal(subkeys[0], (M,))
        b = μ_b + σ_b * random.normal(subkeys[1], (M,))
        e = μ_e + σ_e * random.normal(subkeys[2], (M,))
        # Exponentiate shocks
        a, b, e = jax.tree.map(jnp.exp, (a, b, e))
        # Update the cross-section of firms
        s = update_cross_section(s, a, b, e, firm)

    return s

Let’s try running the code and generating a cross-section.

firm = Firm()
tic()
data = generate_cross_section(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:2.43

2.4374115467071533

We run the function again so we can see the speed without compile time.

tic()
data = generate_cross_section(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:0.87

0.8796219825744629

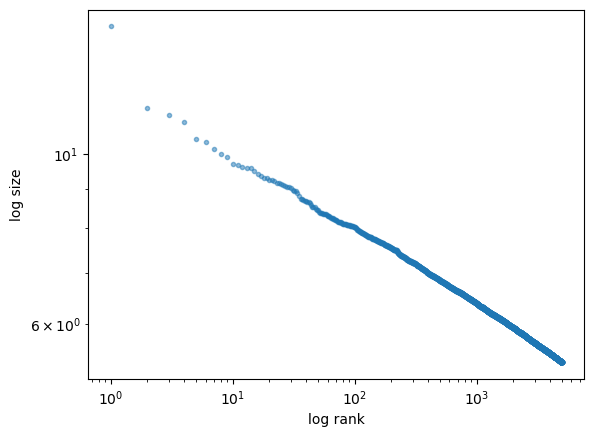
Let’s produce the rank-size plot and check the distribution:

fig, ax = plt.subplots()

rank_data, size_data = qe.rank_size(data, c=0.01)
ax.loglog(rank_data, size_data, 'o', markersize=3.0, alpha=0.5)
ax.set_xlabel("log rank")
ax.set_ylabel("log size")

plt.show()

_images/8366e079dd9b0371a9d1a507adc4492f8e621ad127c717349521c15e4f9abcae.png

The plot produces a straight line, consistent with a Pareto tail.

6.2.1.3. Alternative implementation with `lax.fori_loop`#

Although we JIT-compiled some of the code above, we did not JIT-compile the for loop.

Let’s try squeezing out a bit more speed by

replacing the for loop with lax.fori_loop and
JIT-compiling the whole function.

Here a the lax.fori_loop version:

@jax.jit
def generate_cross_section_lax(
        firm, T=500, M=500_000, s_init=1.0, seed=123
    ):

    μ_a, σ_a, μ_b, σ_b, μ_e, σ_e, s_bar = firm
    key = random.PRNGKey(seed)
    
    # Initial cross section
    s = jnp.full((M, ), s_init)

    def update_cross_section(t, state):
        s, key = state
        key, *subkeys = jax.random.split(key, 4)
        # Generate current random draws 
        a = μ_a + σ_a * random.normal(subkeys[0], (M,))
        b = μ_b + σ_b * random.normal(subkeys[1], (M,))
        e = μ_e + σ_e * random.normal(subkeys[2], (M,))
        # Exponentiate them
        a, b, e = jax.tree.map(jnp.exp, (a, b, e))
        # Pull out the t-th cross-section of shocks
        s = jnp.where(s < s_bar, e, a * s + b)
        new_state = s, key
        return new_state

    # Use fori_loop 
    initial_state = s, key
    final_s, final_key = lax.fori_loop(
        0, T, update_cross_section, initial_state
    )
    return final_s

Let’s see if we get any speed gain

tic()
data = generate_cross_section_lax(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:1.04

1.0461056232452393

tic()
data = generate_cross_section_lax(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:0.06

0.061226844787597656

Here we produce the same rank-size plot:

fig, ax = plt.subplots()

rank_data, size_data = qe.rank_size(data, c=0.01)
ax.loglog(rank_data, size_data, 'o', markersize=3.0, alpha=0.5)
ax.set_xlabel("log rank")
ax.set_ylabel("log size")

plt.show()

6.3. Exercises#

Exercise 6.1

Try writing an alternative version of generate_cross_section_lax() where the entire sequence of random draws is generated at once, so that all of a, b, and e are of shape (T, M).

(The update_cross_section() function should not generate any random numbers.)

Does it improve the runtime?

What are the pros and cons of this approach?

Solution to Exercise 6.1

@jax.jit
def generate_cross_section_lax(
        firm, T=500, M=500_000, s_init=1.0, seed=123
    ):

    μ_a, σ_a, μ_b, σ_b, μ_e, σ_e, s_bar = firm
    key = random.PRNGKey(seed)
    subkey_1, subkey_2, subkey_3 = random.split(key, 3)
    
    # Generate entire sequence of random draws 
    a = μ_a + σ_a * random.normal(subkey_1, (T, M))
    b = μ_b + σ_b * random.normal(subkey_2, (T, M))
    e = μ_e + σ_e * random.normal(subkey_3, (T, M))
    # Exponentiate them
    a, b, e = jax.tree.map(jnp.exp, (a, b, e))
    # Initial cross section
    s = jnp.full((M, ), s_init)

    def update_cross_section(t, s):
        # Pull out the t-th cross-section of shocks
        a_t, b_t, e_t = a[t], b[t], e[t]
        s = jnp.where(s < s_bar, e_t, a_t * s + b_t)
        return s

    # Use lax.scan to perform the calculations on all states
    s_final = lax.fori_loop(0, T, update_cross_section, s)
    return s_final

Here are the run times.

tic()
data = generate_cross_section_lax(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:1.00

1.0009338855743408

tic()
data = generate_cross_section_lax(firm).block_until_ready()
toc()

TOC: Elapsed: 0:00:0.05

0.058072805404663086

This method might or might not be faster.

In general, the relative speed will depend on the size of the cross-section and the length of the simulation paths.

However, this method is far more memory intensive.

It will fail when $T$ and $M$ become sufficiently large.